На сторонах треугольника построены вне него квадраты. Доказать, что отрезок прямой, соединяющий вершины сторон квадратов, выходящих из одной вершины треугольника, в два раза больше медианы треугольника, проведенной из той же вершины

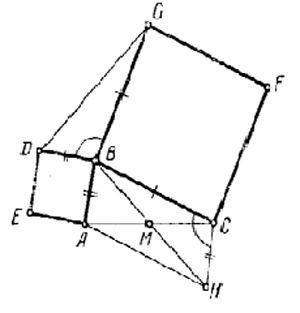
Пусть на сторонах АВ и ВС построены квадраты АВDЕ и BCFG. Продолжим медиану ВМ на отрезок МН, равный ВМ, и проведем прямые НА и НС: четырехугольник АВСН – параллелограмм, так как его диагонали в точке пересечения делятся пополам.

В треугольниках BDG и ВСН DВ = ВА = СН, BG = ВС, ∠DBG = ∠ВСН – как углы с взаимно перпендикулярными сторонами, следовательно, треугольники BDG и ВСН равны, а потому DG = ВН = 2ВМ.