Доказать, что перпендикуляры к хорде, восставленные в ее концах, пересекают произвольный диаметр в точках, которые равно удалены от центра
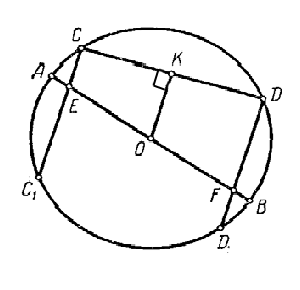
Пусть СС1 и DD1 – перпендикуляры к хорде СD, которые пересекают диаметр АВ в точках Е и F . Для доказательства проведем из центра О ОК перпендикулярно CD, тогда СК = KD. Следовательно, прямая КО проходит через середину К стороны CD прямоугольной трапеции CEFD и параллельна ее сторонам CE и DF, и потому ОК есть ее средняя линия, следовательно, точка О - середина стороны EF и ОЕ = OF.
Похожие примеры: