Определить объем правильной четырехугольной пирамиды, зная угол αее бокового ребра с плоскостью основания и площадь S ее диагонального сечения. Найти также угол, образуемый боковой гранью с плоскостью основания.
Угол α измеряется углом ОBE (рис.), так как OB - проекция ребра BE на плоскость основания.
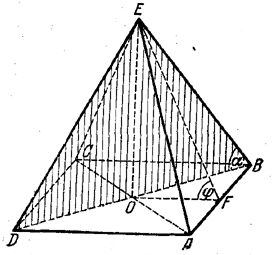
Для построения линейного угла φ двугранного угла при ребре АВ соединим середину F стороны АВ с О и E (см. объяснение к задаче 97). Так как
![]()
то для вычисления V нужно найти Н = ОЕ и d = BD. Из треугольника ОВЕ находим Н = d/2 tg α и, по условию,d/2 Н = S. Перемножив эти равенства, а затем разделив их почленно, найдем
![]()
Следовательно,
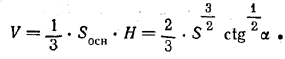
Угoл φ определяем из треугольника OFE, где
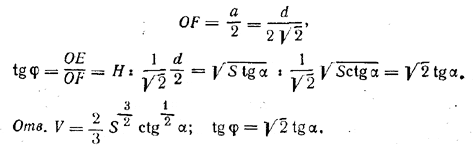
Похожие примеры: