Определить объем правильной четырехугольной пирамиды, боковое ребро которой равно l , а двугранный угол между двумя смежными боковыми гранями равен β.

Проводим высоту ОМ треугольника ОСЕ (рис.); тогда ∠ BMD = β (доказать!).

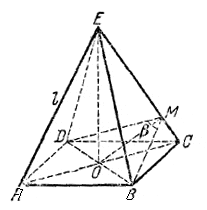
Обозначим ОС= ОВ через х и найeм х из формулы ОС²= СE • СМ, где СE = l и СM = √x² - ОM². Из треугольника ОMВ находим

ОМ = OB • ctg ^β/₂ = x ctg ^β/₂

так что

Подставляя в формулу ОС²= СE • СМ, получаем уравнение

Корень x = 0, очевидно, не соответствует условию, так что имеем

Следовательно,

Н = √CE² - ОC² = √l² - x² = l ctg ^β/₂.

Теперь находим

V = ¹/₃ 2x²H

Замечание. Величина cos β отрицательна, так как ^β/₂ > 45° (ибо tg ^β/₂ = ^OB/_OM = ^OC/_OM , но наклонная ОС больше перпендикуляра ОМ, следовательно, tg ^β/₂ > 1)