В трапеции средняя линия равна 4, а углы при одном из оснований равны 40° и 50°. Найти основания трапеции, если отрезок, соединяющий середины оснований, равен 1.
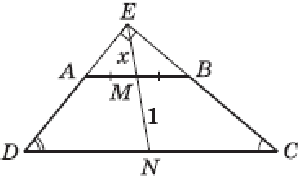
Пусть ABCD — данная трапеция, AB и CD — ее основания (AB < CD), M, N — середины AB и CD соответственно. Пусть также ∠ADC = 50°, ∠BCD = 40°. Средняя линия трапеции равна полусумме оснований, поэтому AB + CD = 8.
Продлим боковые стороны DA и CB до пересечения в точке E. Рассмотрим треугольник ABE, в котором ∠EAB = 50°. ∠EBA = 40°, следовательно, ∠AEB = 90°. Медиана EM этого треугольника, проведенная из вершины прямого угла, равна половине гипотенузы: EM = AM. Пусть EM = x, тогда AM = x, DN = 4 – x.
Согласно условию задачи MN = 1, следовательно, EN = x + 1.
Из подобия треугольников AEM и DEN имеем:
$$ \frac{AM}{DN}=\frac{EM}{EN} \Leftrightarrow \frac{x}{4-x}=\frac{x}{x+1} \Leftrightarrow x=\frac{3}{2} $$Это означает, что AB = 3 и CD = 5.
Похожие примеры: