Выпуклый четырехугольник ABCD описан около окружности с центром в точке O, при этом AO = OC = 1, BO = OD = 2. Найти периметр четырехугольника ABCD.

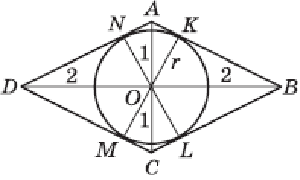
Пусть K, L, M, N — точки касания окружности со сторонами AB, BC, CD, DA соответственно, r — радиус окружности. Так как касательная к окружности перпендикулярна радиусу, проведенному в точку касания, то треугольники AKO, BKO, BLO, CLO, CMO, DMO, DNO, ANO — прямоугольные. Применив к этим треугольникам теорему Пифагора, получим, что

$$ AN=AK=\sqrt{1-r^2}=CL=CM, \\ BK=BL=\sqrt{4-r^2}=DM=DN $$

Следовательно, AB = BC = CD = DA, то есть ABCD — ромб.

Диагонали ромба перпендикулярны друг другу, и точка их пересечения является центром вписанной окружности. Отсюда легко находим, что сторона ромба равна \( \sqrt{1^2 + 2^2} = \sqrt5 \) и значит, периметр ромба равен \(4\sqrt5\)

Ответ:\(4\sqrt5\)