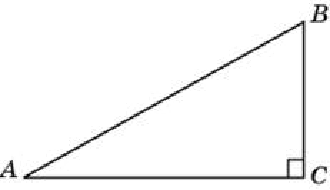
Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.

$$ sinA = \frac{BC}{AB}; \;\; BC = AB\cdot sinA = 25\frac{3}{5} = 5\cdot 3 = 15 $$

Но в задаче просили найти AC. Найдем АС по теореме Пифагора:

$$ AC^2 = AB^2 - BC^2 = 25^2 - 15^2 = 400 $$

AC = 20