На стороне AB параллелограмма ABCD, как на диаметре, построена окружность, проходящая через точку пересечения диагоналей и середину стороны AD. Найдите углы параллелограмма.

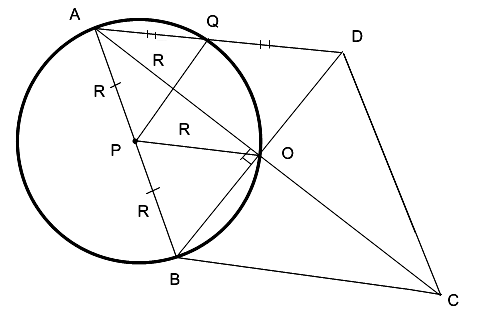
По условию, AB – диагональ => ABCD – ромб

P – середина АВ: по условию Q – середина AD=>PQ – средняя линия
\(\Delta\)ABD=BD=2PQ; PQ=R => BD=2R;

PO=R – средняя линия \(\Delta\)АBD => AD=2·PO=R

\(\Delta\)ABD – правильный => Ответ: 60° и 120°