Вершина C параллелограмма ABCD соединена с точкой N на стороне AB. Отрезок CN пересекает диагональ BD в точке P. Площадь треугольника BNP равна 8, а площадь треугольника BCP равна 12. Найдите площадь параллелограмма ABCD.

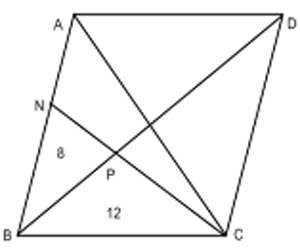
1. Треугольники BNP и BPC имеют общую высоту BH => SBNP/SBPC=PN/PC=>PN/NC=2/3;
2. Треугольники BPN и DPC подобны по двум углам => SBPN/SDPC=(PN/PC)2
   SDPC=9/4; SBPN = (9/4)·8=18;
3. SBCD=SBPC+SDPC=12+18=30;
4. SABCD=2·SBCD=60;

Ответ: 60