В ромбе высота, проведенная из вершины тупого угла, делит сторону ромба пополам. Найдите периметр и высоту ромба, если меньшая диагональ его равна 7

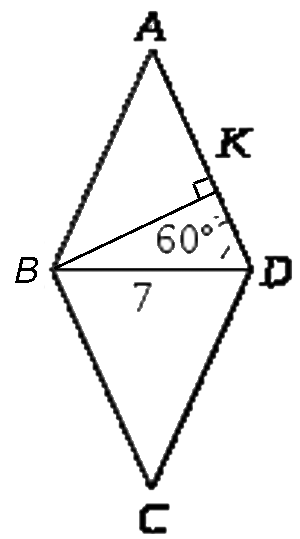
  1. В треугольнике ABD BK – высота и медиана, значит, \(\Delta\)ABD - равнобедренный с основанием AD, т. е. AB = BD = 7 см. Тогда \(\Delta\)ABD - равносторонний, значит, ∠A = ∠ABD = ∠BDA = 60°.
  2. P = 4AB = 4 · 7 = 28 (см).
  3. \(\Delta\)BKD – прямоугольный, BK = AD sin ∠BDK. BK = 7 · sin 60° = \( \frac{7\sqrt3}{2} \) (см).

Ответ: 28 см; 3,5√3 см.





Похожие примеры:
В основании пирамиды лежит прямоугольник с острым углом между диагоналями а (а < 60°), боковые ребра ее равны между собой, а высота h. Внутри этой пирамиды расположена треугольная пирамида, вершина которой совпадает с вершиной первой пирамиды, а вершины основания лежат по одной на трех сторонах прямоугольника. Найти объем четырехугольной пирамиды, если все ребра треугольной пирамиды равны между собой, а боковые грани равновелики. Смотреть решение→
В основании прямой призмы лежит прямоугольный треугольник с катетом а и противолежащим ему углом α. Через вершину прямого угла нижнего основания проведена плоскость, параллельная гипотенузе, под углом β= 90°— α к противолежащей боковой грани и пересекающая ее. Определить объем части призмы между ее основанием и сечением и боковую поверхность призмы, если известно, что боковая грань, проходящая через катет а, равновелика сечению призмы. Определить, при каком значении угла αплоскость сечения пересекает боковую грань, проходящую через гипотенузу основания. Смотреть решение→
На стороне AB параллелограмма ABCD, как на диаметре, построена окружность, проходящая через точку пересечения диагоналей и середину стороны AD. Найдите углы параллелограмма. Смотреть решение→