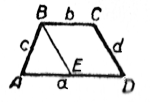
Пусть а - большее основание, А - угол, образованный сторонами а и с. Проведём прямую, параллельную d; тогда трапеция разобьётся на треугольник ABE и параллелограмм BCDE. В треугольнике ABE известны длины трёх сторон: с, d, а - b. По теореме косинусов найдём угол А:

d² = (a - b)² + c²- 2c (a - b) cos А, откуда $$ cosA = \frac{(a - b)^2 + c^2 - d^2}{2d(a - b)} $$

Аналогично вычислим: $$ cosD = \frac{(a - b)^2 + c^2 - d^2}{2d(a - b)} $$ и, наконец, B = \(\pi\) - A ; C = \(\pi\) - D