Центры четырех кругов радиуса rрасположены в вершинах квадрата со стороной а. Найти площадь S общей части всех четырех кругов, заключенной внутри квадрата.

Следует рассмотреть различные случаи в зависимости от величины отношения ^r/_a

1) ^r/_a > √2 . Окружности не пересекают квадрат, S = a².

2) ^√5/₂ < ^r/_a < √2 Очевидно, в этом случае S = a² — 8б,

где б —площадь заштрихованного криволинейного треугольника (рис.).

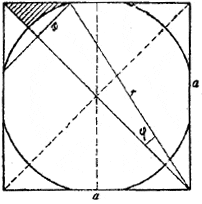
Имеем:

б = ¹/₂a √2x — ¹/₂r² φ,

где φ= arcsin ^x/_r. Для нахождения х заметим, что

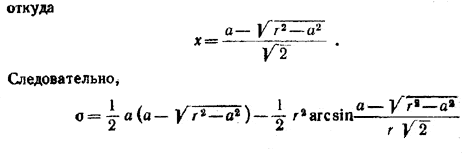
3) ¹/_√2< ^r/_a< ^√5/₂ Здесь S = 8б, где б —площадь заштрихованного криволинейного треугольника (рис.).

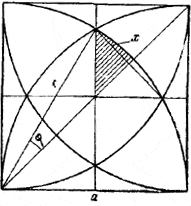
Имеем:

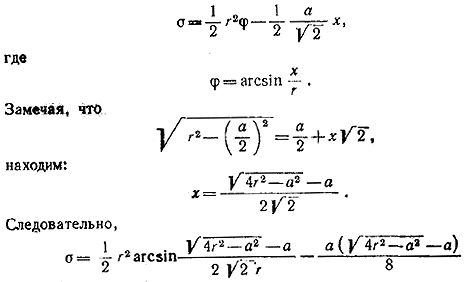
4) ^r/_a< ¹/_√2 Искомая площадь равна нулю.