Диагонали разбивают трапецию на четыре треугольника. Найти площадь трапеции, если площади треугольников, примыкающих к основаниям, равны S₁ и S₂.

Имеем (см. рис.):

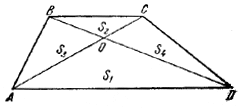
S = S₁ + S₂ + S₃ + S₄. (1)

Далее,

откуда S₃S₄ = S₁S₂. Но, очевидно, имеем

S₃ + S₁ = S₄+ S₁,

так что S₃ = S₄и S₃ = S₄ = √S₁S₂.

Следовательно, из (1) получаем

S = S₁ + S₂ + 2 √S₁S₂= ( √S₁+ √S₂)²