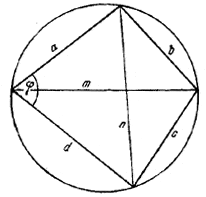
Выразить диагонали вписанного четырехугольника через его стороны. Получить отсюда теорему Птолемея: произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон.

Обозначив через а, b, с, d длины сторон и через m, n.— длины диагоналей четырехугольника (рис.), по теореме косинусов имеем:

n² = a² + d ²—2ad cos φ ,

n² = b² + c² + 2bc cos φ.

Отсюда

(bc + ad) n² = (a² + d ²)bc + (b² + c²) ad = (ab + cd)(ac + bd).

Следовательно,

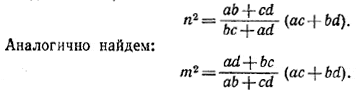
Перемножив эти равенства, получим теорему Птолемея:

mn = ac + bd.