Основание пирамиды — правильный треугольник со стороной а. Одно из боковых ребер перпендикулярно к основанию, а остальные два наклонены к плоскости основания под равными углами β. Найти площадь наибольшей боковой грани пирамиды и угол наклона ее к плоскости основания.

Наибольшую площадь имеет грань ADB (рис.), так как ее высота DE больше высоты DC двух других боковых граней, а основания у всех граней одинаковы.

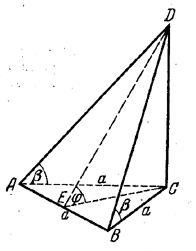
Из треугольника ACD имеем

AD = ^a/_{cos β} и H = a tg β.

Затем находим из треугольника ADE

Угол φ наклона грани ADB к плоскости основания есть ∠ CED (доказать!). Имеем

tg φ = ^H/_EC

где EС = ^a√3/₂