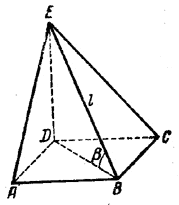
Пирамида имеет в основании квадрат. Из двух противолежащих друг другу ребер одно перпендикулярно к плоскости основания, другое наклонено к ней под углом β и имеет длину l. Определить длины остальных боковых ребер и углы наклона их к плоскости основания пирамиды.

Из треугольника ВDE (рис.), где ∠EBD = β (доказать!), находим

DE = l sin β и BD = l cos β.

Значит,

Из треугольника ADE находим АЕ = √AD² + DE² . Угол φ наклона ребра АЕ к плоскости основания есть ∠DAE (доказать!). Из треугольника ADE имеем tg φ = ^DE/_AD.

Ответ: DE = l sin β;