Внутрь острого угла вписываются круги, касающиеся друг друга. Показать, что радиусы этих кругов образуют геометрическую прогрессию. Найти зависимость между знаменателем прогрессии и величиной острого угла.
Пусть О — вершина острого угла α и Оk—центр й-го круга (рис.).
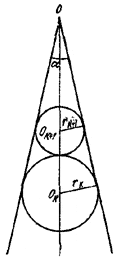
Тогда
rk = OОk sin α/2, rk+1 = (OОk— rk — rk+1) sin α/2
и
rk+1 = rk — rk sin α/2— rk+1 sin α/2.
Следовательно,
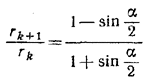
т. е. радиусы кругов образуют геометрическую прогрессию со знаменателем
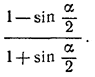
Похожие примеры: