В основании четырехугольной пирамиды лежит ромб, сторона которого равна а и острый угол равен α. Плоскости, проходящие через вершину пирамиды и диагонали основания, наклонены к плоскости основания под углами φи ψ. Определить объем пирамиды, если ее высота пересекает сторону основания.

Пусть ∠ A (рис.) - острый угол ромба, так что АС- большая диагональ и ∠ OAD = ^α/₂

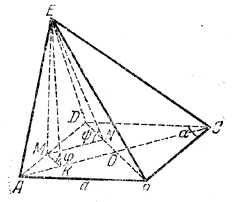
Проведем MK⊥AC и МN⊥ВD. На рис. следует провести MK||BD и MN||AC, так как диагонали ромба взаимно перпендикулярны (ср. предыдущую основу).

Пусть φ есть угол, под которым плоскость EAС, наклонена к плоскости основания. Тогда ∠ МКЕ = φ и ∠MNE = ψ.

Для определения Н выразим МК и MN через Н;

получим MK = H ctg φ и MN = H ctg ψ; эти выражения подставим в соотношение

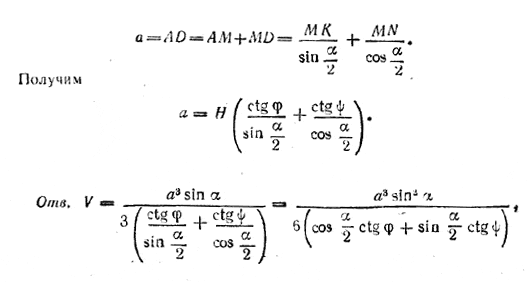
где двугранный угол φ имеет ребром большую диагональ ромба, а угол ψ - меньшую.