Ребро тетраэдра равно b. Через середину одного из ребер проведена плоскость параллельно двум непересекающимся ребрам. Определить площадь полученного сечения.

Пусть секущая плоскость проводится через середину M (рис.) ребра АВ параллельно ребрам АС и BD.

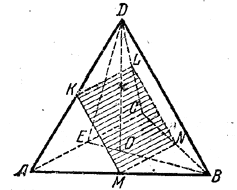
Ребро АС лежит в плоскости ABC. Поэтому плоскость, проведенная через М параллельно АС, пересекает грань ABC по прямой MN, параллельной АС. Значит, MN- средняя линия треугольника ABC ( MN = ¹/₂ AC = ^b/₂) т. е. N есть середина ребра ВС.

Ребро BD лежит в плоскости BCD, а плоскость сечения параллельна ребру BD. Поэтому NL||BD ( NL = ¹/₂BD = ^b/₂ ) и L -середина робра CD.

Так же докажем, что МK= ^b/₂ и что К - середина ребра AD. Следовательно,

KL || АС и KL = ^b/₂.

Значит, сечение MNLK есть ромб. Но кроме того, угол NMK - прямой. Действительно, ребро BD лежит в плоскости BDE (Е - середина АС), а эта плоскость перпендикулярна к ребру АС. Следовательно, BD⊥AC. Но по доказанному MK||BD и MN||AC; значит, MK⊥MN. Из этого следует, чго MNLK, - квадрат со стороной ^b/_{2 .}