В основании прямой призмы лежит трапеция, вписанная в полукруг радиуса R так, что большее основание ее совпадает с диаметром, а меньшее стягивает дугу, равную 2α. Определить объем призмы, если диагональ грани, проходящей через боковую сторону основания, наклонена к основанию под углом α.

Полуокружность изображается полуэллипсом (АВ - какой-либо диаметр эллипса; рис. ).

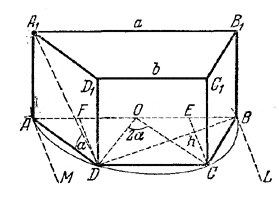
DC проводится параллельно АВ. Прямые, перпендикулярные к АВ, изображаются прямыми, параллельными касательными AM и BL.

Решение. Обозначим АВ = а ; DC = b; DF = CE = h; тогда

По условию a = 2R; сторону b находим по теореме синусов из. треугольника BCD, в котором ∠ DBC измеряется половиной дуги DC = 2α; имеем b = 2R sin α.

Из треугольника ODF, где OD = R, а AOD измеряется дугой , находим

h = FD = R sin (90° - α) = R соs α

Высоту H находим из треугольника A₁AD где ∠ A₁DA = α (доказать!) и AD можно определить из прямоугольного треугольника ADB, где ∠ ABD- опирающийся на дугу AD - равен ( 45° - ^α/₂ ) . Получим

H = 2R sin ( 45° - ^α/₂ ) tg α.

Следовательно,

V = 2R³(1 + sin α) sin ( 45° - ^α/₂ ) tg α cos α,

где можно произвести ряд упрощений:

1 + sin α = 2 cos² ( 45° - ^α/₂ )

и т. д.

Ответ: V = R³ sin 2α cos ( 45° - ^α/₂ )