Через гипотенузу прямоугольного равнобедренного треугольника проведена плоскость P под углом α к плоскости треугольника. Определить периметр и площадь фигуры, которая получится, если спроектировать треугольник на плоскость P. Гипотенуза треугольника равна с.
По условию наклонные АС и CB (рис.) равны.
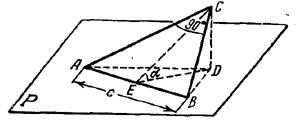
Значит, равны их проекции: AD = DB. Угол DEC (E - середина АВ) есть линейный угол двугранного угла α.
Так как треугольник АСВ прямоугольный при вершине С, то СЕ = АЕ = c/2 . Следовательно, ED = c/2 cos α. Наконец,
AD = BD = √АЕ2+ ЕD2 = c/2√1 + cos2α
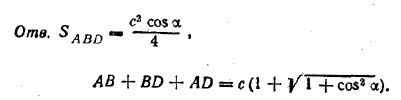
Похожие примеры: