Апофема правильной шестиугольной пирамиды равна m. Двугранный угол при основании равен α. Найти полную поверхность пирамиды.

Соединим середину М стороны АВ с О и S (рис.).

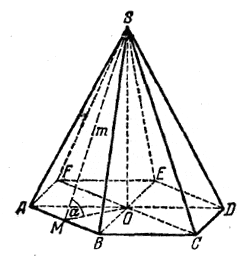
Угол OMS - линейный для двугранного угла αСледовательно,

ОM = SM cos α = m cos α.

Из треугольника АОМ, где ∠ AOM=30°, находим

AM = ^a/₂ = ^√3/₃ • ОМ = ^√3/₃ m cos α.

Далее находим

S_ocн. = 6 (^a/₂)² √3

и

S_бок. = 6 • ^a/₂ • m.

Подставив найденное выражение ^a/₂, получим

S_п = S_ocн. + S_бок. = 2 √3 m² cos α (1 + cos α).

Ответ: S_п = 4 √3 m² cos α cos^{2 α}/₂ .