В правильной треугольной призме угол между диагональю боковой грани и другой боковой гранью равен α. Определить боковую поверхность призмы, зная, что ребро основания равно а.

Для построения угла, образованного диагональю АВ₁ с боковой гранью BB₁C₁C, надо найти проекцию AB₁ на эту грань (рис.).

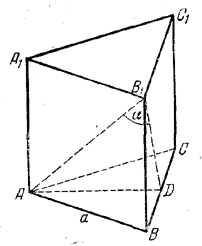
Точка А проектируется в точку D, середину ВС (доказать!). Проекция будет B₁D, так что ∠ AB₁D = a. Из \(\Delta\)B₁BD находим

H = BB₁ = √B₁D² - BD² ;

B₁D найдeм из прямоугольного треугольника AB₁D. Преобразование выражения, полученного для Н, такое же, как в предыдущей задачe