В основании прямой призмы лежит прямоугольный треугольник ABC, у которого ∠C= 90°, ∠A =α и катет АС= b. Диагональ боковой грани призмы, проходящей через гипотенузу АВ, образует с боковой гранью, проходящей через катет АС, угол β. Найти объем призмы.

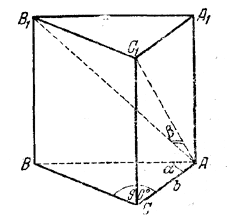
Проекцией диагонали АВ1 на грань АA1С1С будет АС1(рис.), так что ∠B1AC1= β.

Высота призмы

СС1 = √AC12 - AC2 ,

где АС1 определяется из \(\Delta\)В1АС1 имеем





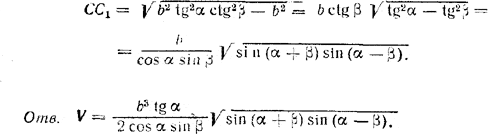
Похожие примеры:
В основании прямой призмы лежит прямоугольный треугольник ABC. Радиус окружности, описанной около него, равен R, катет АС стягивает дугу, равную 2β. Через диагональ боковой грани, проходящей через другой катет ВС, проведена плоскость перпендикулярно к этой грани, образующая с плоскостью основания угол β. Определить боковую поверхность призмы и объем отсеченной четырехугольной пирамиды. Смотреть решение→
В основании прямой призмы ABCA1B1C1 лежит прямоугольный треугольник ABC с углом β при вершине В (β < 45°). Разность между площадями ее боковых граней, проходящих через катеты ВС и АС, равна S. Найти площадь сечения призмы плоскостью, образующей с плоскостью основания угол φ и проходящей через три точки: вершину В1 угла β верхнего основания, середину бокового ребра АА1 и точку D, расположенную на плоскости основания симметрично с вершиной В относительно катета АС. Смотреть решение→
В основании прямой призмы ABCA1B1C1 лежит равнобедренный треугольник ABC с углом αпри основании ВС. Боковая поверхность призмы равна S. Найти площадь сечения призмы плоскостью, проходящей через диагональ боковой грани BCC1B1 параллельно высоте AD основания призмы и образующей с плоскостью основания угол β. Смотреть решение→