Формула объема тела вращения

Рассмотрим тело вращения, полученное вращением вокруг оси абсцисс криволинейной трапеции, которая соответствует неотрицательной непрерывной функции

у = f(x), х \( \in \) [а; b] (рис. 250).

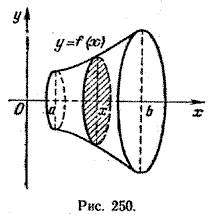
Очевидно, что сечение этого тела плоскостью, проходящей через точку с абсциссой

х \( \in \) [а; b] и перпендикулярной оси Ох, есть круг радиуса f(x). Следовательно,

S(x) = π f ²(x)

а объем рассматриваемого тела вращения вычисляется по формуле

$$ V = \pi\int_{a}^{b}f^2(x)dx $$

Задача 1. Найти объем тела, полученного вращением вокруг оси Ох криволинейной трапеции, соответствующей функции у = х³, х \( \in \) [1; 3] (рис. 251).

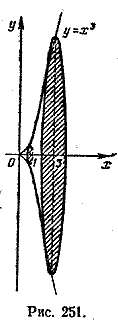
По формуле получаем

$$ V = \pi\int_{1}^{3}x^6dx = \left.\frac{\pi}{7}x^7\right|_1^3 = \frac{\pi}{7}(3^7 - 1) $$

Ответ: \( V=\frac{2186}{7}\pi \)

Задача 2. Найти объем тела, полученного вращением вокруг оси абсцисс криволинейной трапеции, соответствующей функции у = cos х , х \( \in \) [-^π/₂; ^π/₂] (рис. 252).

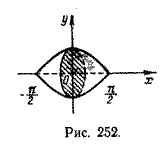
По формуле получаем

$$ V = \pi\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}cos^2x dx =\\= \frac{\pi}{2}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}(1+cos2x)dx = \frac{\pi^2}{2} $$

Ответ: \( V=\frac{\pi^2}{2} \)

Задача 3. Найти объем тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями у = √3x , у = ^x/₂ и x = 3 (рис. 253).

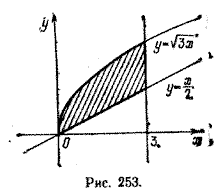
Очевидно, что объем данного тела вращения равен разности объемов тел, полученных вращением криволинейных трапеций, соответствующих функциям у = √3x и у = ^x/₂,

х \( \in \) [0; 3]. Следовательно,

$$ V = \pi\int_{0}^{3}3x dx - \pi\int_{0}^{3}\frac{x^2}{4}dx =\\= \left.\frac{3\pi}{2}x^2\right|_0^3 - \left.\frac{\pi}{12}x^3\right|_0^3 = \frac{27}{2}\pi - \frac{27}{12}\pi = \frac{45}{4}\pi $$

Ответ: \( V=\frac{45}{4}\pi \)