Подобие конусов и цилиндров

Определение. Два цилиндра или конуса называются подобными, если они произошли от вращения подобных прямоугольников или прямоугольных треугольников вокруг сходственных сторон.

Пусть h и h₁ будут высоты двух подобных цилиндров или конусов, r и r₁ - радиусы их оснований, l и l₁ - образующие;

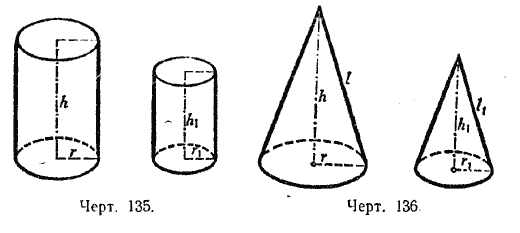
тогда согласно определению

$$ \frac{r}{r_1} = \frac{h}{h_1} \;\;и\;\; \frac{r}{r_1} = \frac{l}{l_1}, $$

откуда (по свойству равных отношений) находим:

$$ \frac{r+h}{r_1 + h_1} = \frac{r}{r_1} \;\;и\;\; \frac{r + l}{r_1 + l_1} = \frac{r}{r_1}, $$

Заметив эти пропорции, докажем следующую теорему.

Теорема. Боковые и полные поверхности подобных цилиндров или конусов относятся, как квадраты радиусов или высот; объёмы - как кубы радиусов или высот.

Пусть S, Т и V будут соответственно боковая поверхность, полная поверхность и объём одного цилиндра или конуса; S₁, Т₁ и V₁ -те же величины для другого цилиндра или конуса, подобного первому. Тогда будем иметь для цилиндров:

$$ \frac{S}{S_1} = \frac{2\pi rh}{2\pi r_1 h_1} =\\= \frac{rh}{r_1 h_1} = \frac{r}{r_1}\cdot \frac{h}{h_1} =\\= \frac{r^2}{{r_1}^2} = \frac{h^2}{{h_1}^2} $$
$$ \frac{T}{T_1} = \frac{2\pi r(r+h)}{2\pi r_1(r_1 + h_1)} =\\= \frac{r}{r_1}\cdot \frac{r+h}{r_1 + h_1} =\\= \frac{r^2}{{r_1}^2} = \frac{h^2}{{h_1}^2} $$
$$ \frac{V}{V_1} = \frac{\pi r^2 h}{\pi {r_1}^2 h_1} =\\= \frac{r^2}{{r_1}^2}\cdot \frac{h}{h_1} =\\= \frac{r^3}{{r_1}^3} = \frac{h^3}{{h_1}^3} $$

для конусов:

$$ \frac{S}{S_1} = \frac{\pi rl}{\pi r_1 l_1} =\\= \frac{r}{r_1}\cdot \frac{l}{l_1} =\\= \frac{r^2}{{r_1}^2} = \frac{h^2}{{h_1}^2} $$
$$ \frac{T}{T_1} = \frac{\pi r(r+l)}{\pi r_1(r_1 + l_1)} =\\= \frac{r}{r_1}\cdot \frac{r+l}{r_1 + l_1} =\\= \frac{r^2}{{r_1}^2} = \frac{h^2}{{h_1}^2} $$
$$ \frac{V}{V_1} = \frac{\frac{1}{3}\pi r^2 h}{\frac{1}{3}\pi {r_1}^2 h_1} =\\= \frac{r^2}{{r_1}^2}\cdot \frac{h}{h_1} =\\= \frac{r^3}{{r_1}^3} = \frac{h^3}{{h_1}^3} $$