Площадь поверхности цилиндра и его объем

Площадь поверхности цилиндра

Площадь каждого основания цилиндра равна πr², площадь обоих оснований составит 2πr² (рис.).

Площадь боковой поверхности цилиндра равна площади прямоугольника, основание которого равно 2πr, а высота равна высоте цилиндра h, т. е. 2πrh.

Полная поверхность цилиндра составит: 2πr² + 2πrh = 2πr (r + h).

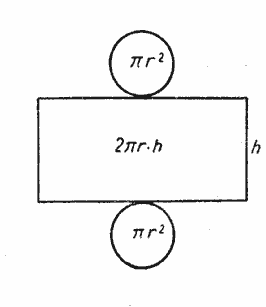
За площадь боковой поверхности цилиндра принимается площадь развертки его боковой поверхности.

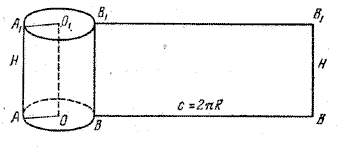
Поэтому площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис.) и вычисляется по формуле

S _б.ц. = 2πRH, (1)

где R — радиус основания, а H — высота цилиндра.

Если к площади боковой поверхности цилиндра прибавить площади двух его оснований, то получим площадь полной поверхности цилиндра

S_полн. =2πRH + 2πR² = 2πR (H + R).

Объем прямого цилиндра

Теорема. Объем прямого цилиндра равен произведению площади его основания на высоту, т. е.

V = QH,

где Q — площадь основания, а Н — высота цилиндра.

Так как площадь основания цилиндра равна Q, то существуют последовательности описанных и вписанных многоугольников с площадями Q_n и Q’_n таких, что

\(\lim_{n \rightarrow \infty}\) Q_n = \(\lim_{n \rightarrow \infty}\) Q’_n = Q.

Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H. Эти призмы являются описанными и вписанными для данного цилиндра. Их объемы находятся по формулам

V_n = Q_nH и V’_n = Q’_nH.

Следовательно,

V= \(\lim_{n \rightarrow \infty}\) Q_nH = \(\lim_{n \rightarrow \infty}\) Q’_nH = QH.

Следствие.
Объем прямого кругового цилиндра вычисляется по формуле

V = π R²H

где R — радиус основания, а H — высота цилиндра.

Так как основание кругового цилиндра есть круг радиуса R, то Q = π R², и поэтому

V = QH = π R²H.