Площадь поверхности конуса

Площадь поверхности конуса (или просто поверхность конуса) равна сумме площадей основания и боковой поверхности.

Площадь боковой поверхности конуса вычисляется по формуле: S = πRl, где R — радиус основания конуса, а l — образующая конуса.

Так как площадь основания конуса равна πR² (как площадь круга), то площадь полной поверхности конуса будет равна: πR² + πRl = πR (R + l ).

Получение формулы площади боковой поверхности конуса можно пояснить такими рассуждениями. Пусть на чертеже изображена развёртка боковой поверхности конуса. Разделим дугу АВ на возможно большее число равных частей и все точки деления соединим с центром дуги, а соседние — друг с другом хордами.

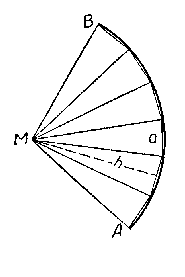
Получим ряд равных треугольников. Площадь каждого треугольника равна ^ah/₂ , где а — длина основания треугольника, a h — его высота.

Сумма площадей всех треугольников составит: ^ah/₂ • n = ^anh/₂ , где n — число треугольников.

При большом числе делений сумма площадей треугольников становится весьма близкой к площади развёртки, т. е. площади боковой поверхности конуса. Сумма оснований треугольников, т. е. an, становится весьма близкой к длине дуги АВ, т. е. к длине окружности основания конуса. Высота каждого треугольника становится весьма близкой к радиусу дуги, т. е. к образующей конуса.

Пренебрегая незначительными различиями в размерах этих величин, получаем формулу площади боковой поверхности конуса (S):

S = ^Cl/₂, где С — длина окружности основания конуса, l — образующая конуса.

Зная, что С = 2πR, где R — радиус окружности основания конуса, получаем: S = πRl.

Примечание. В формуле S = ^Cl/₂ поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы это равенство считать приближённым. Но в старших классах средней школы доказывается, что равенство

S = ^Cl/₂ точное, а не приближённое.

Теорема. Боковая поверхность конуса равна произведению длины окружности основания на половину образующей.

Впишем в конус (рис.) какую-нибудь правильную пирамиду и обозначим буквами р и l числа, выражающие длины периметра основания и апофемы этой пирамиды.

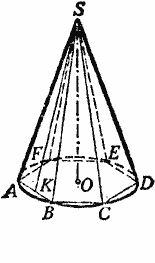
Тогда боковая поверхность её выразится произведением ¹/₂ р • l .

Предположим теперь, что число сторон вписанного в основание многоугольника неограниченно возрастает. Тогда периметр р будет стремиться к пределу, принимаемому за длину С окружности основания, а апофема l будет иметь пределом образующую конуса (так как из ΔSAK следует, что SA — SK< AK); значит, если образующую конуса обозначим буквой L, то боковая поверхность вписанной пирамиды, постоянно равная

¹/₂ р• l, будет стремиться к пределу ¹/₂С• L. Этот предел и принимается за величину боковой поверхности конуса. Обозначив боковую поверхность конуса буквой S, можем написать:

S = ¹/₂С • L = С • ¹/₂L

Следствия.
1) Так как С = 2πR, то боковая поверхность конуса выразится формулой:

S = ¹/₂• 2πR • L = πRL

2) Полную поверхность конуса получим, если боковую поверхность сложим с площадью основания; поэтому, обозначая полную поверхность через Т, будем иметь:

T = πRL + πR² = πR(L + R)

Теорема. Боковая поверхность усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую.

Впишем в усечённый конус (рис.) какую-нибудь правильную усечённую пирамиду и обозначим буквами р, р₁ и l числа, выражающие в одинаковых линейных единицах длины периметров нижнего и верхнего оснований и апофемы этой пирамиды.

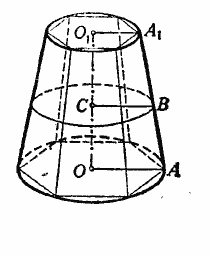
Тогда боковая поверхность вписанной пирамиды равна ¹/₂ (р + р₁) • l

При неограниченном возрастании числа боковых граней вписанной пирамиды периметры р и р₁ стремятся к пределам, принимаемым за длины С и С₁ окружностей оснований, а апофема l имеет пределом образующую L усечённого конуса. Следовательно, величина боковой поверхности вписанной пирамиды стремится при этом к пределу, равному (С + С₁) L. Этот предел и принимается за величину боковой поверхности усечённого конуса. Обозначив боковую поверхность усечённого конуса буквой S, будем иметь:

S = ¹/₂ (С + С₁) L

Следствия.
1) Если R и R₁ означают радиусы окружностей нижнего и верхнего оснований, то боковая поверхность усечённого конуса будет:

S = ¹/₂ (2πR + 2πR₁) L = π (R + R₁) L.

2) Если в трапеции OO₁А₁А (рис.), от вращения которой получается усечённый конус, проведём среднюю линию ВС, то получим:

ВС = ¹/₂(OA + O₁A₁) = ¹/₂ • (R + R₁),

откуда

R + R₁ = 2ВС.

Следовательно,

S = 2πBC• L,

т. е. боковая поверхность усечённого конуса равна произведению длины окружности среднего сечения на образующую.

3) Полная поверхность Т усечённого конуса выразится так:

T = π( R² + R₁² + RL + R₁L)