Объем конуса

Объём конуса выражается такой же формулой, что и объём пирамиды: V = ¹/₃ Sh,

где V — объём конуса, S — площадь основания конуса, h — его высота.

Окончательно V = ¹/₃ πR²h, где R — радиус основания конуса.

Получение формулы объёма конуса можно пояснить таким рассуждением:

Пусть дан конус (рис). Впишем в него правильную пирамиду, т. е. построим внутри конуса такую пирамиду, вершина которой совпадает с вершиной конуса, а основанием служит правильный многоугольник, вписанный в основание конуса.

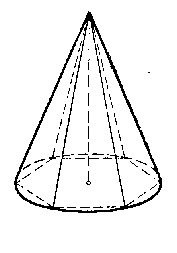
Объём этой пирамиды выразится формулой: V’ = ¹/₃ S’h, где V — объём пирамиды,

S’ — площадь её основания, h — высота пирамиды.

Если при этом за основание пирамиды взять многоугольник с очень большим числом сторон, то площадь основания пирамиды будет весьма мало отличаться от площади круга, а объём пирамиды — весьма мало отличаться от объёма конуса. Если, пренебречь этими различиями в размерах, то объём конуса выразится следующей формулой:

V = ¹/₃ Sh, где V — объём конуса, S — площадь основания конуса, h — высота конуса.

Заменив S через πR², где R — радиус круга, получим формулу: V = ¹/₃ πR²h, выражающую объём конуса.

Примечание. В формуле V = ¹/₃ Sh поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы его считать приближённым, но в старших классах средней школы доказывается, что равенство

V = ¹/₃ Sh точное, а не приближённое.

Объем произвольного конуса

Теорема. Объем произвольного конуса равен одной трети произведения площади основания на высоту, т.е.

V = ¹/₃QH, (1)

где Q — площадь основания, а Н — высота конуса.

Рассмотрим конус с вершиной S и основанием Ф (рис.).

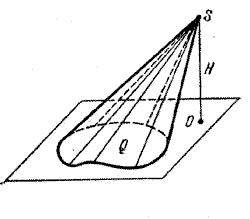
Пусть площадь основания Ф равна Q, а высота конуса равна Н. Тогда существуют последовательности многоугольников Ф_n и Ф’_n с площадями Q_n и Q’_n таких, что

Ф_n ⊂ Ф_n ⊂ Ф’_n и \(\lim_{n \rightarrow \infty}\) Q’_n = \(\lim_{n \rightarrow \infty}\) Q_n = Q.

Очевидно, что пирамида с вершиной S и основанием Ф’_n будет вписанной в данный конус, а пирамида с вершиной S и основанием Ф_n — описанной около конуса.

Объемы этих пирамид соответственно равны

V_n = ¹/₃Q_nH , V’_n = ¹/₃Q’_nH

Так как

\(\lim_{n \rightarrow \infty}\) V_n = \(\lim_{n \rightarrow \infty}\) V’_n = ¹/₃QH

то формула (1) доказана.

Следствие. Объем конуса, основанием которого является эллипс с полуосями а и b, вычисляется по формуле

V = ¹/₃ π abH (2)

В частности, объем конуса, основанием которого является круг радиуса R, вычисляется по формуле

V = ¹/₃ π R²H (3)

где Н — высота конуса.

Как известно, площадь эллипса с полуосями а и b равна π ab, и поэтому формула (2) получается из (1) при Q = π ab. Если а = b = R, то получается формула (3).

Объем прямого кругового конуса

Теорема 1. Объем прямого кругового конуса с высотой Н и радиусом основания R вычисляется по формуле

V = ¹/₃ π R²H

Данный конус можно рассматривать как тело, полученное вращением треугольника с вершинами в точках О(0; 0),В(Н; 0), А(Н; R) вокруг оси Ох (рис.).

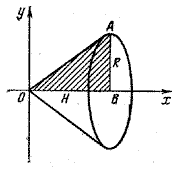
Треугольник ОАВ является криволинейной трапецией, соответствующей функции

у = ^R/_H х, х ∈ [0; H]. Поэтому, используя известную формулу, получаем

$$ V=\pi\int_{0}^{H}(\frac{R}{H}x)^2dx=\\=\frac{\pi R^2}{H^2}\cdot\frac{x^3}{3}\left|\begin{array}{c}H\\\\ 0\end{array}\right.=\\=\frac{1}{3}\pi R^2H $$

Следствие. Объем прямого кругового конуса равен одной трети произведения площади основания на высоту, т. е.

V = ¹/₃ QH

где Q — площадь основания, а H — высота конуса.

Теорема 2. Объем усеченного конуса с радиусами оснований r и R и высотой H вычисляется по формуле

V = ¹/₃ πH( r ² + R² + rR).

Усеченный конус можно получить вращением вокруг оси Ох трапеции О ABC (рис.).

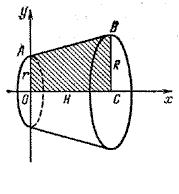
Прямая АВ проходит через точки (0; r) и (H; R), поэтому она имеет уравнение

$$ y=\frac{R-r}{H}x + r $$

получаем

$$ V=\pi\int_{0}^{H}(\frac{R-r}{H}x + r)^2dx $$

Для вычисления интеграла сделаем замену

$$ u=\frac{R-r}{H}x + r, du=\frac{R-r}{H}dx $$

Очевидно, когда х изменяется в пределах от 0 до H, переменная и изменяется от r до R, и поэтому

$$ V=\pi\int_{r}^{R}u^2\frac{H}{R-r}du=\\=\frac{\pi H}{R-r}\cdot\frac{u^3}{3}\left|\begin{array}{c}R\\\\ r\end{array}\right.=\\=\frac{\pi H}{3(R-r)}(R^3-r^3)=\\=\frac{1}{3}\pi H(R^2 + r^2 + Rr) $$