Цилиндрические поверхности

Если через каждую точку кривой L провести прямую, параллельно данному вектору а, то получим поверхность, которая называется цилиндрической поверхностью. Прямые, параллельные вектору а и принадлежащие цилиндрической поверхности, называются образующими этой поверхности, а кривая L называется направляющей цилиндрической поверхности (рис. 225).

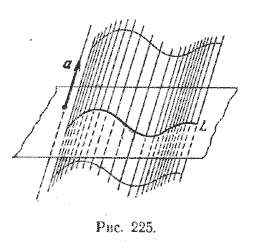
Если в сечении цилиндрической поверхности плоскостью, перпендикулярной к ее образующим, (в нормальном сечении) получается окружность, то цилиндрическая поверхность называется круговой. Если в сечении получается эллипс, то цилиндрическую поверхность называют эллиптической, если гипербола - гиперболической, если парабола - параболической.

Пусть в пространстве дана прямоугольная система координат Oxyz, и пусть в плоскости хОу дана кривая L, уравнение которой в этой плоскости имеет вид

F(x;y) = 0. (1)

Составим уравнение цилиндрической поверхности с образующими, параллельными вектору a = (α; β; γ), γ =/= 0, если за направляющую принята кривая L (рис.226).

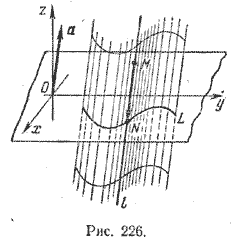
Рассмотрим произвольную точку этой поверхности М(х; у; z). Образующая l, проходящая через точку М, пересечет плоскость хОу в точке N, лежащей на кривой L. Если координаты точки N в пространстве обозначить (х₁; у₁; 0), то вектор \(\overrightarrow{MN}\) имеет координаты

(x₁ - x; у₁- у ; 0 - z).

По определению цилиндрической поверхности векторы а и \(\overrightarrow{MN}\) коллинеарны, т. е.

\(\overrightarrow{MN}\) = λ a ,

следовательно, имеем систему уравнений

x₁ - x = λα, у₁- у = λβ, 0 - z = λγ.

Решив эту систему уравнений относительно λ, x₁и у₁, получим

λ = - ^z/_γ x₁ = x - z ^α/_γ , у₁ = у - z ^β/_γ. (2)

Так как точка N лежит на кривой L, то F(х₁; у₁) = 0. Заменив х₁ и у₁ по формулам (2), получим уравнение

F(x - z ^α/_γ; у - z ^β/_γ) = 0, (3)

которое, очевидно, и будет уравнением данной цилиндрической поверхности.

Задача 1. Составить уравнение цилиндрической поверхности, у которой направляющая лежит в плоскости хОу и имеет уравнение х² + у² = 4, а образующие параллельны вектору а = (0; 1; 1).

Так как, согласно условию задачи F(x; у) = х² + у² - 4 и α = 0, β = 1, γ = 1, то в силу формулы (3) уравнение данной цилиндрической поверхности имеет вид

( x - z ⁰/₁ )² + ( у - z ¹/₁ )² - 4 = 0

или, окончательно,

х² + ( у - z)² - 4 = 0.

Эта поверхность изображена на рис. 227.

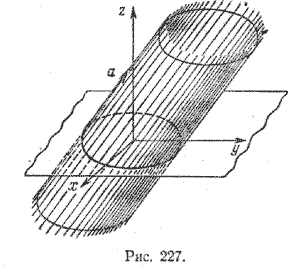
Аналогично можно показать, что если направляющая цилиндрической поверхности L лежит в плоскости xOz и определяется уравнением F(x; z) = 0, а вектор а не параллелен этой плоскости, то цилиндрическая поверхность имеет уравнение

F(x - y ^α/_β ; z - y ^γ/_β ) = 0

Наконец, если L определяется уравнением F(у; z) = 0 и а не параллелен плоскости yOz, то уравнение цилиндрической поверхности имеет вид

F(y - x ^β/_α ; z - x ^γ/_α ) = 0

Отметим, что если направляющая цилиндрической поверхности лежит в плоскости

хОу, а образующие параллельны оси Oz, то уравнение цилиндрической поверхности в пространстве совпадает с уравнением направляющей и имеет вид

F(x; y) = 0. (4)

Уравнение (4), как уравнение множества точек плоскости, определяет кривую L, в то же самое время уравнение (4), как уравнение множества точек пространства, определяет цилиндрическую поверхность.

Итак, каждое из уравнений

F(x; y) = 0, F(x; z) = 0, F(y; z) = 0

можно истолковать двояко: если это уравнение множества точек плоскости, то это уравнение линии L, лежащей в плоскости своих переменных; если же это уравнение множества точек пространства, то каждое из этих уравнений определяет цилиндрическую поверхность с направляющей L и образующими, параллельными оси oтсутствующей переменной.

Рассмотрим несколько примеров.

1. Уравнение

х² + у² = r²

на плоскости хОу определяет окружность с центром в начале координат и радиусом r (рис. 228, а).

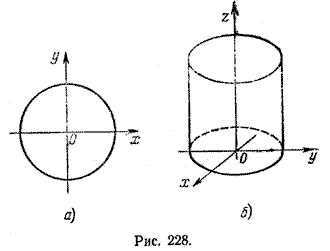
Это жe уравнение в пространстве определяет круговую цилиндрическую поверхность, направляющей которой является окружность, лежащая в плоскости хОу, а образующие параллельны оси Oz (рис. 228, б).

2. Уравнение

х² + z² = 4

на плоскости xOz определяет окружность с центром в начале координат и радиусом

r = 2 (рис. 229, а).

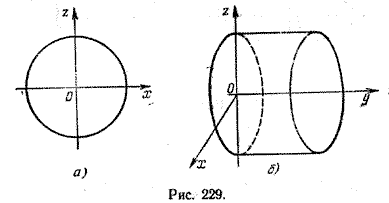
Это же уравнение в пространстве определяет круговую цилиндрическую поверхность, направляющей которой является окружность, лежащая в плоскости xOz, а образующие параллельны оси Оу (рис. 229, б).

3. Уравнение

y² + z² + 9 = 0

и на плоскости, и в пространстве определяет пустое множество, так как сумма неотрицательных чисел не может быть числом отрицательным.

4. Уравнение

$$ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $$

на плоскости хОу определяет эллипс с центром в начале координат и полуосями а и b (рис. 230, а).

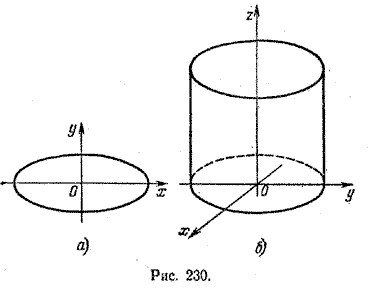
Это же уравнение в пространстве определяет эллиптическую цилиндрическую поверхность с направляющей в плоскости хОу и образующими, параллельными оси Oz (рис. 230, б).

5. Уравнение

$$ \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 $$

на плоскости хОу определяет гиперболу с центром в начале координат и полуосями а и b (рис. 231, а).

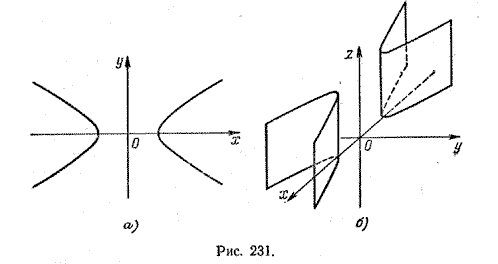
В пространстве это уравнение определяет гиперболическую цилиндрическую поверхность с образующими, параллельными оси Oz (рис. 231, б).

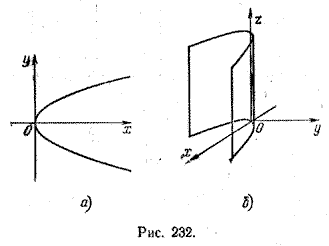
6. Уравнение

y² = 2рх

на плоскости хОу определяет параболу (рис. 232, а), а в пространстве - параболическую цилиндрическую поверхность с образующими, параллельными оси Oz (рис. 232, б).

Задача 2. Определить вид поверхности 3x² + 6y² - 24 = 0.

Данное уравнение приведем к виду:

$$ \frac{x^2}{8}+\frac{y^2}{4}=1 $$

Это уравнение в пространстве определяет эллиптическую цилиндрическую поверхность с направляющей в плоскости хОу и образующими, параллельными оси Oz.