Около правильной шестиугольной пирамиды описан конус. Найти его объем, если ребро пирамиды равно l и плоский угол между двумя соседними боковыми ребрами равен α.
Из \(\Delta\)ASB (рис.) находим AB = 2l sin α/2;
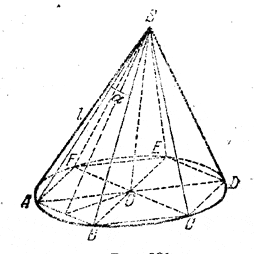
следовательно, R=OA=AB=2l sin α/2. Из \(\Delta\)ASO находим
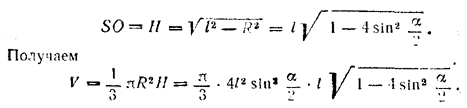
Подкоренное выражение Можно преобразовать к виду, удобному для логарифмирования, как в задаче 557; получим
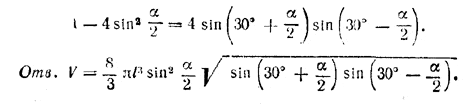
Похожие примеры: