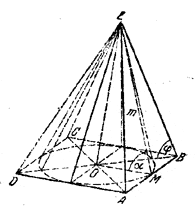
Боковые грани правильной четырехугольной пирамиды наклонены к основанию под углом α. Апофема пирамиды равна m. Найти полную поверхность конуса, вписанного в пирамиду, а также угол наклона бокового ребра к основанию.
Из треугольника ОМЕ (рис.) имеем
ОМ = r = m cos α; ЕО = Н = m sin α.
По формуле Sп. = πr (r + l ). где l = m, находим
Sп. = πm2 cos α (1 + cos α)
или
Sп. = 2πm2 cos α cos2 α/2
Угол φ = ∠ ЕВО, под которым боковое ребро BE наклонено к основанию, определяем из треугольника ЕВО, где ОВ = ОМ√2 = m √2 cos α. Имеем
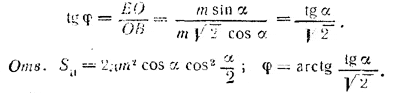
Похожие примеры: