Будем считать, что все образующие конуса, касающиеся шаров, касаются одновременно двух шаров - внутреннего и внешнего. Проведем сечение через вершину конуса S и центры двух шаров, касающихся одной образующей

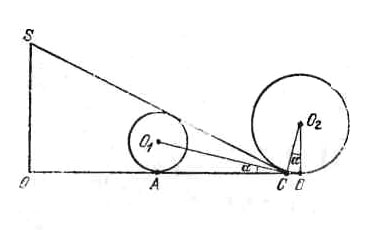
Из условия, что n шаров радиуса R касаются друг друга, следует равенство

$$ |OA| = \frac{R}{sin\frac{\pi}{n}} $$

аналогично

$$ |OB| = \frac{2R}{sin\frac{\pi}{n}} $$

. Следовательно,

$$ |AB|=a=\frac{R}{sin\frac{\pi}{n}} $$

Пусть |АС| = x. Тогда

$$ tg\alpha = \frac{R}{x},\;\;ctg\alpha = \frac{2R}{a - x} $$

Перемножив эти равенства, получим уравнение для х:

$$ x^2-ax+2R^2 = 0 $$

откуда

$$ x_1=\frac{a-\sqrt{a^2-8R^2}}{2},\;\;x_2=\frac{a+\sqrt{a^2-8R^2}}{2},\\ \text{где}\;\;a=\frac{R}{sin\frac{\pi}{n}} $$

Условие \(a^2 - 8R^2 \geq 0\) приводит к неравенству

$$ sin\frac{\pi}{n}\leq\frac{1}{2\sqrt2} $$

Кроме того, должно выполняться неравенство tg а = R/x < 1. Теперь нетрудно получить, что корень х₁ подходит, если

$$ \frac{1}{3}\lt sin\frac{\pi}{n}\leq\frac{1}{2\sqrt2} $$

Для корня х₂ остается одно ограничение:

$$ sin\frac{\pi}{n}\leq\frac{1}{2\sqrt2} $$

Можно доказать, что

$$ \frac{1}{3}\lt sin\frac{\pi}{n}\leq\frac{1}{2\sqrt2} \text{лишь при}\;\;n=9 $$

Объем конуса будет равен

$$ \frac{1}{3}\pi(a+x)^3tg2\alpha $$

Выражая a, x и tg2α по соответствующим формулам через R и n, получим ответ:

$$ V=\frac{\pi R^3(3+\sqrt{1-8sin^2\frac{\pi}{n}})^3(1+\sqrt{1-8sin^2\frac{\pi}{n}})}{12sin^2\frac{\pi}{n}(1-6sin^2\frac{\pi}{n}+\sqrt{1-8sin^2\frac{\pi}{n}})},\;\;n\geq9 $$

Кроме того, при n = 9 возможно еще одно значение:

$$ \frac{\pi R^3(3-\sqrt{1-8sin^2\frac{\pi}{9}})^3(1-\sqrt{1-8sin^2\frac{\pi}{9}})}{12sin^2\frac{\pi}{9}(1-6sin^2\frac{\pi}{9}+\sqrt{1-8sin^2\frac{\pi}{9}})} $$