Опустим перпендикуляры А₁М и В₁М на CD, B₁N и С₁N на AD, С₁К и D₁K на АВ, D₁L и A₁L на СВ.

Поскольку

$$\frac{|A_1M|}{|B_1M|}=\frac{|B_1N|}{|NC_1|}=\frac{|C_1K|}{|KD_1|}=\frac{|D_1L|}{|A_1L|}=\frac{1}{3}$$

(эти отношения равны косинусу двугранного угла при ребре тетраэдра) и |А₁В₁| = |В₁С₁| = |C₁D₁| = |D₁A₁|, то должны выполняться равенства |А₁М| = |B₁N| = |С₁К| = |D₁L| = х, |В₁М| = |NC₁| = |KD_1| = | A₁L| = Зх (на рис. ниже изображена развертка тетраэдра). Каждое ребро CD, DA, АВ, ВС окажется разделенным на отрезки m и n так, как показано на рисунке.

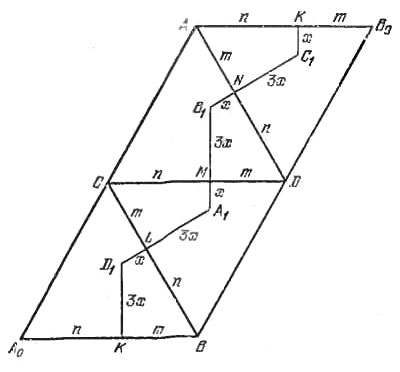
Учитывая, что m + n = a, найдем

$$x = \frac{a\sqrt3}{12},\;\;m=\frac{5a}{12},\;\;n=\frac{7a}{12}$$

после чего найдем объем тетраэдра A₁B₁C₁D₁.

Ответ: $\frac{a^3\sqrt2}{162}$