Пусть в треугольнике АВС стороны ВС, СА и АВ равны соответственно a, b и c. Из того, что пирамиды АВСС₁, АВВ₁С₁ и АА₁В₁С₁ равны, следует, что в каждой из них есть по две грани, равных треугольнику АВС.

В самом деле, если в каждой пирамиде была бы одна такая грань, то между вершинами пирамид АВСС₁ и А₁В₁С₁А было бы соответствие А -> А₁, В -> В₁, С -> С₁, С₁ -> А, т.е. |СС₁| = |АС₁|, |ВС₁| - |В₁А|, а это означало бы, что в пирамиде АВС₁В₁ нет ни одной грани, равной ΔАВС. Теперь нетрудно заключить, что боковое ребро призмы равно или а, или b, или c (если, например, ΔАС₁В = ΔАВС, то в пирамиде А₁В₁С₁А грань А₁В₁А соответствует грани АС₁В пирамиды АВСС₁ и ΔА₁В₁А = ΔАВС).

Разберем все возможные случаи.

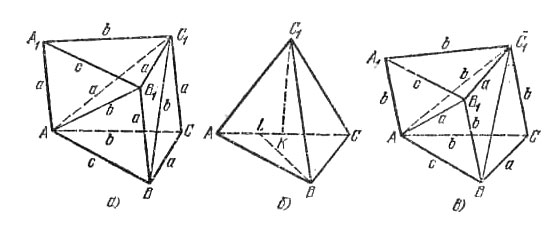
1) |АА₁| = |ВВ₁| = |CC₁| = а (рис. а). Тогда из вершины С пирамиды АВСС₁ выходят два ребра длины a и одно длины b, а ребру СС₁ противолежит ребро длины c. Отсюда следует, что вершине С пирамиды ABСС₁ должна соответствовать вершина С, пирамиды А₁В₁С₁А и |АС₁| = a. Теперь можно заключить, что |АВ₁| = |ВС₁| = b.

Во всех трех пирамидах двугранные углы при ребрах, имеющих длину b, равны, при этом два этих угла в сумме дают π (два угла, например, при ребре С₁В в пирамидах АВСС₁ и АВВ₁С₁), т. е. каждый из них равен π/2.

Проведем перпендикуляры BL и С₁К к ребру АС (рис. б). Поскольку двугранный угол при ребре АС - прямой, то

$$ b^2 = |C_1B|^2 = |C_1K|^2 + |KL|^2+|LB|^2 =\\= |C_1C|^2 - |KC|^2 + (|KC|-|LC|)^2 +|BC|^2 - |LC|^2 = 2a^2 - bx $$

где x = |LC|, и находится из уравнения

$$ a^2 - x^2 = c^2 -(b-x)^2, \;\; x=\frac{a^2+b^2-c^2}{2b} $$

Таким образом, \(3a^2 - 3b^2 + c^2 = 0\). Но ΔАВС по условию прямоугольный. Это возможно лишь при условии \(c^2 = a^2 + b^2\). Следовательно, \(b = а\sqrt2,\;\; с = a\sqrt3\).

Теперь можно найти двугранный угол при ребре ВС нашей призмы. ∠АСС₁ = π/4 является линейным углом этого двугранного угла (треугольники АВС и С₁СВ - прямоугольные, с прямыми углами при вершине С). Двугранный угол при ребре АВ пирамиды ABCC₁ равен π/3. Покажем это. Пусть этот угол равен φ. Тогда двугранный угол при ребре АВ призмы АВСА₁B₁С₁ равен 2φ, а при ребре А₁В₁ - равен φ, таким образом,

$$ 3\phi = \pi,\;\;\;\phi = \frac{\pi}{3} $$

2) |АА₁| = |ВВ₁| = |СС₁| = b (рис. в). В этом случаи в пирамиде АВСС₁ из вершины С выходят два ребра длины b и одно длины a. Значит, такая же вершина есть и в пирамиде A₁B₁С₁A. Это может быть или вершина А, или C₁. В обоих случаях получаем |АВ₁| = a, |АС₁| = b (напоминаем, что должны найтись две грани со сторонами a, b и c). Таким образом, в пирамидах АВСC₁

и A₁B₁C₁A имеется по одной грани, представляющей из себя правильный треугольник со стороной b, в то время как в пирамиде АВВ₁С₁ такой грани нет, чему бы ни равнялось ребро ВС₁. Таким образом, этот случай невозможен.

3) |AA₁| = |ВВ₁| = |СС₁| = c. Этот случай, по существу, совпадает с 1-м, только основания АВС и А₁В₁С₁ меняются местами.

Ответ:\(\frac{\pi}{2},\;\;\frac{\pi}{4}(\text{или}\;\;\frac{3\pi}{4}),\;\;\frac{\pi}{3}(\text{или}\;\;\frac{2\pi}{3})\).