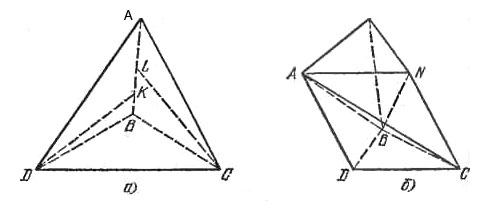
Докажем сначала, что двугранные углы при ребрах DB и АС равны π/2. Пусть |AD| = |CD| = |ВС| = а. |BD| = |AС| = b, |АВ| = c, b > a. Опустим из D и С перпендикуляры DK и CL на ребро АВ (рнс., а).

Обозначим |АК| = |BL| = |x|, |KL| = |c - 2х|, |DK| = |CL| = h.

Поскольку двугранный угол при ребре АВ равен π/3 то |DC|² = |DK|² + |CL|² - |DK| • |CL| + |KL|², т. е.

$$ a^2 = h^2+(c-2x)^2 $$

заменяя

$$ h^2=a^2-x^2 $$

получим \(3x^2-4cx+c^2=0\), откуда \(x_1=\frac{c}{3},\;\;x_2=c\)

Из условия b > a следует, что x < c/2, значит, x = c/3. Таким образом, величины a, b и с связаны соотношением

$$ c^2=3(b^2 - a^2) $$

Найдем площади треугольников ABD и ACD:

$$ S_{ABD} = S_{ABC} = \frac{1}{2}c\sqrt{a^2-\frac{c^2}{9}}=\frac{1}{2}c\sqrt{\frac{4a^2-b^2}{3}},\\S_{ACD} = S_{BDC} = \frac{1}{4}b\sqrt{4a^2-b^2} $$

Выражая объем тетраэдра ABCD через двугранный угол при ребре АВ и площади граней ABD и АВС, а затем через φ - двугранный угол при ребре АС (он также равен углу при ребре BD) и площади граней АВС и ACD, получим

$$ V_{ABCD}=\frac{1}{3}\frac{S_{ABD}S_{ABC}}{|AB|}\cdot\frac{\sqrt3}{2}=\frac{1}{3}\frac{S_{ACD}S_{ABC}}{|AC|}sin\phi $$

откуда

$$ sin\phi = \frac{S_{ABD}}{S_{ACD}}\frac{|AC|}{|AB|}\cdot\frac{\sqrt3}{2}=\\=\frac{2c\sqrt{\frac{4a^2-b^2}{3}}}{b\sqrt{4a^2-b^2}}\cdot \frac{b}{c}\cdot\frac{\sqrt3}{2}=1 $$

Значит, \(\phi = \frac{\pi}{2}\).

Для определения суммы трех оставшихся двугранных углов рассмотрим призму BCDMNA (рис., б). Тетраэдр ABCN равен тетраэдру ABCD, поскольку плоскость АВС перпендикулярна плоскости ADCN, ADCN - ромб, следовательно, тетраэдры ABCD и ABCN симметричны относительно плоскости BСА. Точно так же тетраэдр ABMN симметричен тетраэдру ABCN относительно плоскости ABN (угол при ребре BN в тетраэдре ABCN равен углу при ребре BD тетраэдра ABCD, т. е. равен π/2), следовательно, тетраэдр ABMN равен тетраэдру ABCN и равен исходному тетраэдру ABCD.

Двугранные углы призмы при ребрах CN и ВМ равны соответственно двугранным углам при ребрах DC и ВС тетраэдра ABCD. А поскольку сумма двугранных углов при боковых ребрах треугольной призмы равна π, сумма двугранных углов при ребрах AD, DC и СВ тетраэдра ABCD также равна π, а сумма всех двугранных углов тетраэдра, исключая данный угол при ребре АВ, равна 2π.