Дан тетраэдр ABCD. Другой тетраэдр - A1B1C1D1 расположен так, что его вершины А1, В1, С1, D1 лежат соответственно в плоскостях BCD, CDA, DAB, АВС, а плоскости его граней A1B1C1, B1C1D1, C1D1A1, D1A1B1 содержат соответственно вершины D, А, В и С тетраэдра ABCD. Известно также, что A1 совпадает с центром тяжести треугольника BCD, а прямые BD1, СВ1, DC1 делят пополам соответственно отрезки АС, AD, АВ. Найти объем общей части этих тетраэдров, если объем тетраэдра ABCD равен V.
Пусть К, L и М - середины ребер AB, AC и AD (рис.).
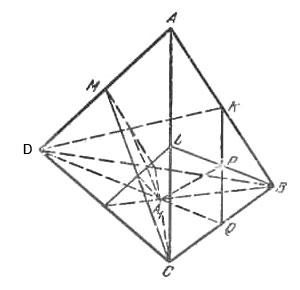
Тогда из условия задачи следует, что тетраэдр A1B1C1D1 ограничивают плоскости DKA1, BLA1, СМА1 и плоскость, проходящая через А параллельно BCD. При этом вершины B1, С1 и D1 расположены так, что точки М, К и L являются серединами СВ1, DC1 и BD1 (на рисунке точки B1, С1, D1 отсутствуют).
Пусть теперь Q - середина ВС, Р - точка пересечения BL и KQ. Для того чтобы найти объем общей части двух пирамид ABCD и A1B1C1D1, мы должны от объема пирамиды ABCD - V - отнять объемы трех пирамид, равновеликих DKBQ (каждая из них имеет объем 1/4V), и прибавить объемы трех пирамид, равновеликих A1BQP. Объем последней пирамиды равен \(\frac{1}{24}V\). Таким образом, объем общей части равен \(\frac{3}{8}V\)
Похожие примеры: