Дан куб ABCDA₁B₁C₁D₁. Плоскость, проходящая через А и касающаяся вписанного в куб шара, пересекает ребра А₁В₁ и A₁D₁ в точках К и N. Определить величину двугранного угла между плоскостями АС₁К и AC₁N.

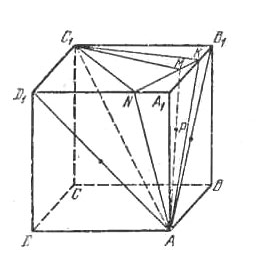
Пусть плоскость AKN касается шара в точке Р, а прямая АР пересекает NK в точке М (рис.). Тогда плоскость С₁NA является биссекторной плоскостью двугранпого угла, образованного плоскостями D₁С₁А и С₁МА (плоскости D₁AN и ANM касаются шара, а плоскости D₁C₁A и С₁МА проходят через его центр).

Точно так же плоскость С₁КА является биссекторной плоскостью двугранного угла, образованного плоскостями МС₁A и С₁В₁A. Таким образом, двугранный угол между плоскостями AС₁К и AС₁N вдвое меньше двугранного угла между плоскостями АВ₁С₁ и AB₁С₁, равного 2π/3.

Ответ: π/3.