Рассмотрим пирамиду SABC (рис.), в которой |СА| = |AB|, ∠ВАС = 2π/n, SA перпендикулярна плоскости АВС, и такую, что вершина А проектируется на плоскость SBC в точку О - центр окружности, вписанной в SBC.

Впишем в эту пирамиду конус так, что его вершина совпадает с А, а окружностью его основания является окружность, вписанная в SBC. Очевидно, что если мы возьмем n таких пирамид, основания которых расположены на плоскости АВС так, что их основания, равные ΔАВС, образуют правильный n-угольник с центром в А, то конусы, вписанные в эти пирамиды, образуют нужную нам систему конусов.

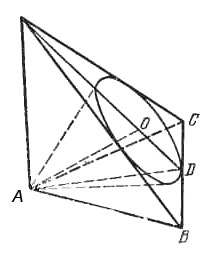
Далее, пусть D - середина ВС, |OD| = r, |AD| = l. Тогда \(|SD| = \frac{l^2}{r},\;\;|BD| = l tg\frac{\pi}{n}\). Поскольку ∠SBD = 2∠0BD, tg ∠SBD = \(\frac{|SD|}{|BD|}=\frac{l}{r tg\frac{\pi}{n}},\\ tgOBD=\frac{r}{ltg\frac{\pi}{n}}\), можно составить уравнение

$$ \frac{l}{r tg\frac{\pi}{n}}=\frac{2\frac{r}{l tg\frac{\pi}{n}}}{1-\frac{r^2}{l^2tg^2\frac{\pi}{n}}} $$

откуда

$$ \frac{r}{l} = \frac{tg\frac{\pi}{n}}{\sqrt{1+2tg^2\frac{\pi}{n}}} $$

Ответ:

$$ 2arcsin\frac{tg\frac{\pi}{n}}{\sqrt{1+2tg^2\frac{\pi}{n}}} $$