В треугольнике АВС ВМ и CN – биссектрисы внешних углов В и С, АМ и AN – перпендикуляры, опущенные из вершины А соответственно на ВМ и CN. Доказать, что длина отрезка MN равна полупериметру треугольника АВС

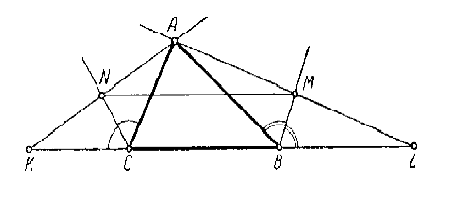
Пусть ВМ – биссектриса внешнего угла ABL, а CN – биссектриса угла АСК, АМ⊥ВМ, AN⊥CN.

В треугольнике ABL биссектриса ВМ – еще и высота, а потому треугольник ABL – равнобедренный и АВ = BL, АМ = ML.

Аналогично АС = СК и AN = NK. Следовательно, Р_АВС= АВ + ВС + СА = BL + BC + CK = KL.

В треугольнике KAL отрезок MN – средняя линия, а потому MN = 1/2KL = 1/2P_АВС