На отрезке прямой АВ взята точка С. По одну сторону АВ восставлены к ней перпендикуляры АА1 = ВС и ВВ1 = АС, а по другую СС1 = АВ. На стороне А1В1 треугольника А1В1С1 строится квадрат по ту же сторону от А1В1, что и вершина С1; аналогично строятся квадраты на сторонах В1С1 и С1А1. Доказать, что точки пересечения диагоналей каждого квадрата совпадают соответственно с точками С, А и В.
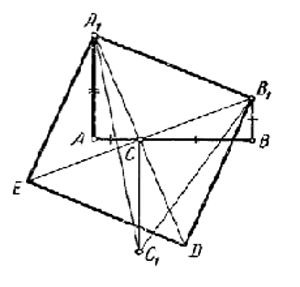
Соединим прямыми точки А1, В1 с точкой С. По двум катетам треугольника АА1С и ВВ1С равны, откуда А1С = В1С1 при этом ∠В1СВ + ∠А1СА = 90°, и, следовательно, ∠А1СВ1 = 90°, а потому в равнобедренном треугольнике А1СВ1 ∠СА1В1 = СВ1А1 = 45° и С – точка пересечения диагоналей квадрата А1В1DE, причем она лежит на прямой АВ. Аналогично доказывается для других квадратов.
Похожие примеры: