АА₁ – высота равнобедренного треугольника АВС с основанием ВС, CD – биссектриса. Проведены DE⊥BC, DF⊥CD до пересечения со стороной ВС. Доказать, что А₁Е = 1/4 CF.

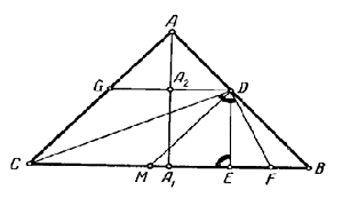
Проведем прямую DG параллельно стороне ВС, которая пересечет высоту АА₁ в точке А₂.

Тогда ЕА₁ = DA₁ = 1/2GD (1), так как треугольник ADG – равнобедренный и его высота АА₁ есть медиана.

Пусть DM – медиана прямоугольного треугольника CDF, тогда СМ = MD = MF (2) и ∠GCD = ∠CDM, следовательно, DM||AC. Из равенств (1) и (2) получим, что FC = 2MC = 2GD = 4EA₁, откуда ЕА₁ = 1/4FC.