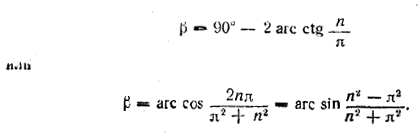Определить угол между осью и образующей такого конуса, у которого полная поверхность в n раз больше площади осевого сечения.

Площадь осевого сечения есть RH. Полная поверхность πRl + πR². По условию .

Если β - угол между осью и образующей, то R = l sin β и H = l cos β. Подставляя эти выражения, получим

Это уравнение можно решить различными способами; короче всего применить формулу ; мы получим

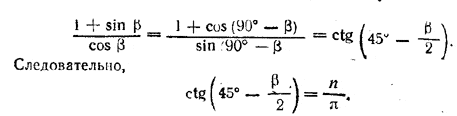
Отсюда можно определить угол 45° - ^β/₂ а затем и угол β.

Однако не при всяком n задача имеет решения. Действительно, угол β заключен в границах от 0 до 90°; значит, угол 45° - ^β/₂ заключен между 0 и 45°, т. е. величина ⁿ/_π = =ctg ( 45° - ^β/₂ ) непременно должна быть больше единицы, т. е. должно быть n > π. При n = 1, 2, 3 задача не имеет решения.

Замечание. Уравнение

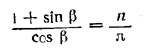
можно решить еще так. Представим его в виде ⁿ/_πcos β -1 = sin β, возведем в квадрат обе части равенства и заменим sin² β через 1- cos² β. Получим два решения: одно из них, cos β = 0, будет посторонним (оно является решением уравнения ⁿ/_πcos β -1 = -sin β; другое решение

совпадает с предыдущим.

Однако теперь легко прийти к ошибочному выводу, что задача имеет решение также и при n = 1, 2, 3. Ведь при любом положительном значении п величина заключена между 0 и 1 Поэтому в пределах от 0 до 90° всегда найдется угол косинус которого равен

Ошибка этого рассуждения состоит в следующем. Из соотношения и данного уравнения следует, что .

Отсюда видно, что должно быть n > π (в противном случае угол β будет отрицательным, что невозможно).

Ответ: Если n < π, то задача не имеет решения. Если n > π, то