В конус вписан шар. Отношение их объемов равно n. Найти угол наклона образующей к основанию (вычислить при n = 4).

При обозначениях рис. имеем

¹/₃ πR²H = n • ⁴/₃ πr

Подставляя сюда

r = R tg ^α/₂ и H = R tg α,

получим уравнение

tg α = 4n tg^{3 α}/₂.

Применив формулу

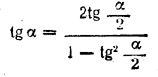
и обозначив tg ^α/₂ через z, получим уравнение

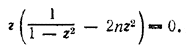
Оно распадается на два, но одно из них (z = 0) не согласуется с условием (угол α не может равняться нулю).

Другое уравнение приводится к виду z⁴- z² + ¹/_2n = 0, т. е. совпадает с уравнением предыдущей задачи. Получаем два решения:

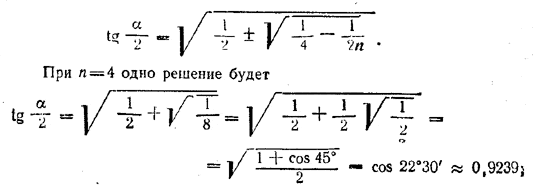
другое дает

tg ^α/₂ = sin 22°30’ ≈ 0,3827

(отсюда α₁ ≈ 85°28’ и α₂ ≈ 41°53’).

Ответ: Тот же, что в предыдущей задаче.

При n = 4 имеем

α₁ =2 arc tg (cos 22° 30’) (≈85° 28’);

α₂ = 2arctg (sin 22°30’) (≈41° 53’).