Полная поверхность прямого кругового конуса в n раз больше поверхности вписанного в него шара. Под каким углом образующие этого конуса наклонены к плоскости его основания?
При обозначениях рис. условие задачи выражается равенством
πR ( l + R ) = n • 4πr2.
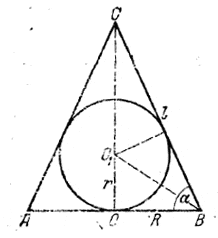
Из треугольника OBO1 находим r = R tg α/2 , а из треугольника ВОС имеем ВС = l = R/cos α
Предыдущее равенство по сокращении на πR2 примет вид
1 + 1/cos α = 4n tg2 α/2
Применим формулу
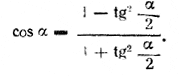
Будем иметь уравнение
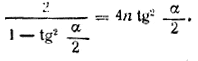
Положив tg α/2 = z, получим
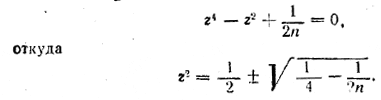
(Освобождаясь от знаменателя, мы могли бы внести лишнее решение ( tg2 α/2 = 1 ) , но такого решения мы не получаеи: оно не удовлетворяет исходному уравнению.)
Отсюда видно, что при n < 2 задача не имеет решения (под корнем отрицательное число). При n > 2 оба значения величины z 2 положительны 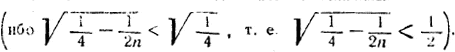
Так как величина tg α/2 должна быть положительной, то можем иметь только два решения:
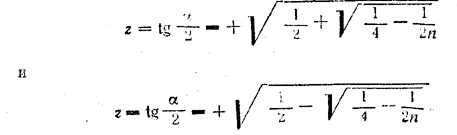
Так как угол α/2 меньше 45°, то tg α/2 должен быть меньше единицы; знaчит, должно быть z 2 < 1. Но это неравенство всегда соблюдено, ибо
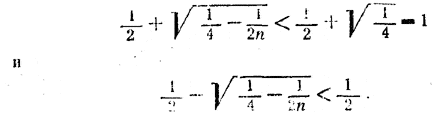
Ответ: Задача имеет решение только при n > 2. При n >2 имеем два решения:
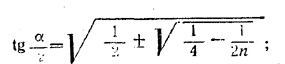
при n =2 оба решения совпадают![]()