Из середины высоты правильной четырехугольной пирамиды опущен перпендикуляр на боковое ребро, равный h, и перпендикуляр на боковую грань, равный b. Найти объем пирамиды.

План решения: из подобия треугольников OEL и МЕК. (рис.) выразим OL через МК=b и ME = ^H/₂, из подобия треугольников ОСЕ и MEN выразим ОС через MN = h и ME = ^H/₂ .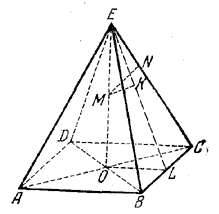

Подставив найденные выражения в соотношение OC²=2• OL² получим уравнение, из которого найдем Н.

Решение. Имеем

OL : Н = МК : ЕК,

т. е.