Секущая плоскость делит боковые ребра треугольной пирамиды в отношениях (считая от вершины) \( \frac{m_1}{n_1}, \frac{m_2}{n_2}, \frac{m_3}{n_3} \). В каком отношении эта плоскость разделит объем пирамиды?
Пусть (рис.)
![]()
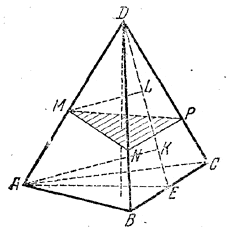
Найдем сначала отношение объема V1 пирамиды DMNP к объему V пирамиды DABC. Примем грань BDC за основание пирамиды DABC и грань NPD за основание пирамиды DMNP. Пусть ребро DA проектируется на плоскость DBC отрезком, лежащим на прямой DE. Тогда точки А и М проектируются в некоторые точки К и L, лежащие на прямой DE. Следовательно, высоты AK= h и ML = h1 лежат в плоскости ADE и треугольники DML и DAK подобны. Значит,
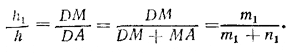
Площадь S1 основания NDP относится к площади S основания BDC, как DN•DP к DB•DC (так как треугольники NDP и BDC имеют общий угол D ). Значит,
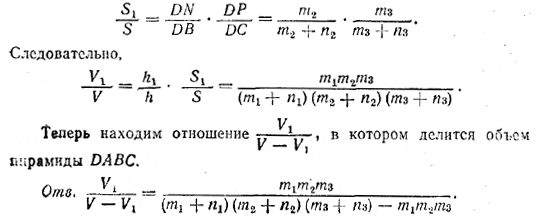
Похожие примеры: