Доказать, что в прямоугольном треугольнике сумма катетов равна сумме диаметров вписанной и описанной окружностей.

Диаметр 2R окружности, описанной около прямоугольного треугольника AВС (рис.), равен гипотенузе АВ.

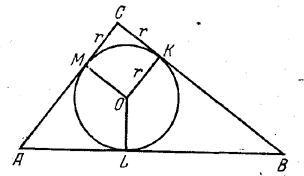
Диаметр 2r вписанной окружности равен МС + СК (так как МОКС есть квадрат). Следовательно,

АС+ВС = (АМ+ВК) + (МС+СК) = (AL+LB) + (МС+СК) =2R+2r.