Доказать, что в прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой, опущенными на гипотенузу.

Так как ∠DCA = ∠OBC (рис.) и ∠BCO = ∠OBC (ибо медиана ОС равна половине гипотенузы), то ∠DCA = ∠BCO.

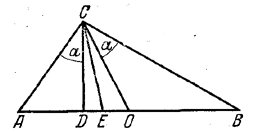
Но по условию ∠ACE = ∠BCE. Вычитая из этого равенства предыдущее, получаем ∠DCE = ∠OCE, т. е. СЕ делит пополам угол DCO.