В круг вписан правильный 2n-угольник; вокруг этого же круга описан правильный n-угольник. Площади этих многоугольников отличаются друг от друга на Р. Определить радиус круга.

Площадь правильного вписанного 2n - угольника равна nR² sin ^180°/_n . Площадь правильного описанного n-угольника равна nR² tg ^180°/_n

По условию

nR² (tg ^180°/_n - sin ^180°/_n ) = P

Отсюда

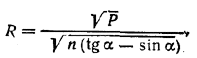
где α = ^180°/_n . Выражение tg α - sin α можно преобразовать так:

tg α - sin α = tg α ( l - cos α) =2 tg α sin^{2 α}/₂.